TLSH - Technical Overview

by Jonathan Oliver
12 / April / 2021.

Introduction

Intended Audience

In this page, we explain the technical details behind TLSH. We hope that this content is useful to researchers / academics and security experts who wish to understand the technical details for TLSH. In addition, we offer technical rationales for the design decisions in TLSH.

List of Papers/Presentations

This overview is based on content from the following conference presentations:
Title Conference Topic
TLSH--a locality sensitive hash CTC 2013 Defines TLSH. Including (i) How to calculate TLSH for a file and (ii) How to calculate the distance between two TLSH digests.
Using randomization to attack similarity digests ATIS 2014 Does experiments attacking TLSH, SSDEEP and SDHASH.
HAC-T and fast search for similarity in security COINS 2020 Considers how you do Nearest Neighbour search for matches to a TLSH digest.
Uses the Nearest Neighbour searech for a fast clustering algorithm (HAC-T).
Scalable Malware Clustering using Multi-Stage Tree Parallelization ISI 2020 Scalable Clustering of TLSH digests.
Designing the Elements of a Fuzzy Hashing Scheme Presented at EUC/Trustcom 2021 Explains the design of TLSH focussing on why TLSH uses the parameters it does.
Fast Clustering of High Dimensional Data Clustering the Malware Bazaar Dataset Needs to be submitted Detailed explanation of clustering using the TLSH distance score and the HAC-T algorithm. Analysis of the Malware Bazaar dataset.

TSLH Technical Overview

TLSH is a fuzzy hash. At first glance it would appear to be similar to other fuzzy hashes like SSDEEP and SDHASH. When selecting a fuzzy hash, some of the criteria that should be considered are: According to these criteria, TLSH rates well: TLSH is different from other fuzzy hashes in the following ways:

Fast Nearest Neighbour Search and Scalable Clustering

The key to nearly all fast search methods is to use an index which will typically take the form of a binary tree. An example TLSH tree is shown in figure 1.

Figure 1. A TLSH Tree

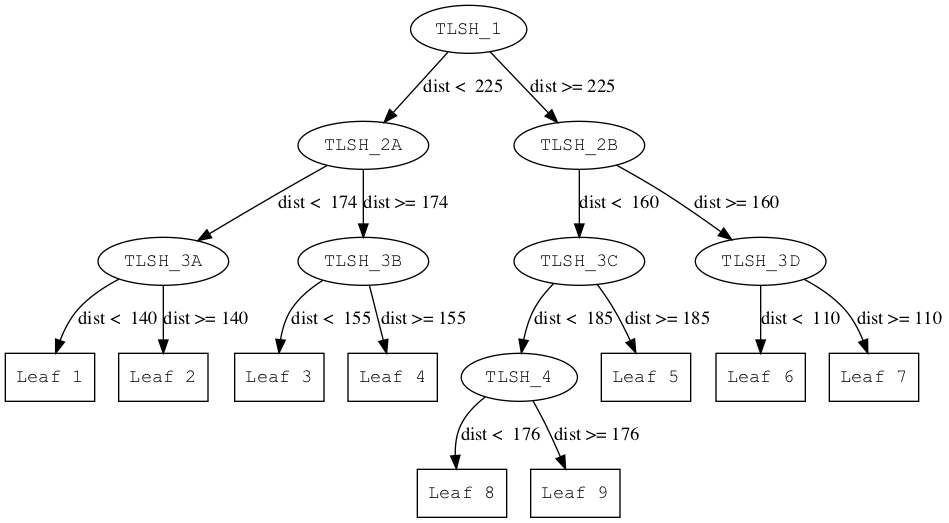Each node has a TLSH node and a distance threshold. The meaning of the root node from Figure 1 (with contents TLSH_1 and threshold T=225) is:

If we are searching for the nearest neighbour for a search TLSH value (S), then we can traverse a TLSH tree and find a leaf using the Search algorithm in Figure 2 (from HAC-T and fast search for similarity in security).

Figure 2. Search Algorithm

As described in that paper, there are 2 approaches to using TLSH for fast search:

  1. A backtrack policy can be used to guarantee that the closest item(s) in the tree are found; or
  2. A forest of such trees can be built to arrive at an approximate nearest neighbour search. Experiments have found that using forests with of the order of 10 trees achieves good results.

Scalable Clustering

Consider clustering a data set D with N samples in it with a Cluster Distance CDist (CDist means that we will merge clusters which have items within distance CDist of each other).

Normally hierarchical clustering is an infeasible approach to use for clustering since it requires a pre-processing step of finding the closest neighbour for each item which is O(N2).
It is possible to use the fast search capabilities of a TLSH tree (or forest) to do fast hierarchical clustering. Using the TLSH tree, we can find the closest neighbours in O(log N). Thus to find the closest item for all N items is a O(N log N) operation which scales well to large datasets.
We have called the algorithm to do this HAC-T and it is shown in Figure 3 below.


Figure 3. The HAC-T Clustering Algorithm

Using trees and the HAC-T algorithm for other Similarity Digests

The preceeding sections lead us to ask the question, "Why is not a similar approach used for other fuzzy hashes such as SSDEEP and SDHASH?". The reason is that (for the vast majority of datasets) similarity measures will identify a small number of items as having a high similarity score and everything else has a similarity score of 0 (or the score which defines "not similar"). So if such similarity based methods are used to build a tree, it will be unbalanced as shown in Figure 4:

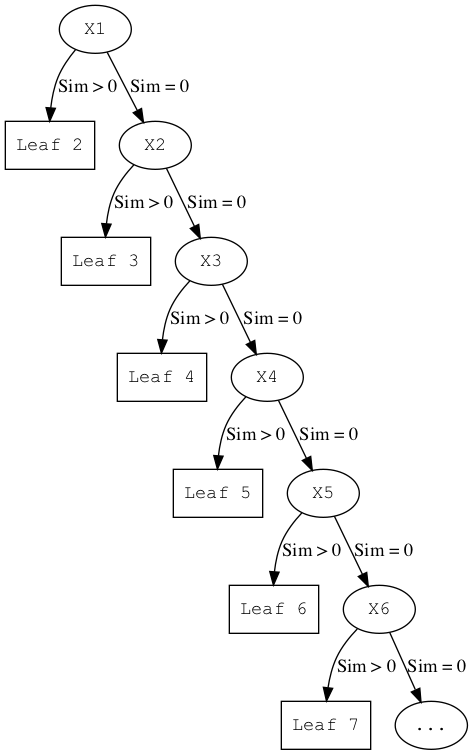Figure 4. Similarity measures lead to unbalanced trees

Once the tree is unbalanced, the search reduces to being like a linear search through a linked list. This is not a scalable solution.

In addition, to really use the capabilities of such a tree for fast search, the criteria being used should be a distance metric to enable the use of Vantage Point Trees.

But isn't a Similarity Score just a Negative Distance Score?

In many papers where authors wished to compare and evaluate TLSH with similarity digests such as SSDEEP and SDHASH, authors would negate the TLSH distance in an attempt to make the score compatible using functions such as:
Similarity(TLSH_1, TLSH_2) = 100 - distance(TLSH_1, TLSH_2) and if the Simiarity was negative then treat it as zero.

We suggest that cutting off scores in this way should be avoided (or only used in a careful manner). This is because fast search and fast clustering are such valuable capabilities.

Robustness to Attack

During the design of TLSH, we made attacking the hash a part of the design process. We give more extensive details in 2 papers, and will summarise it here.

We considered a range of file types:

We considered modifications which were consistent with these files types. So for text files, we looked at changes such as changing the case of letters, changing how lines were split and substituting one word for another. For executable files, we considered changes such as changing the ordering of functions, swapping the arrangement of IF statements, and adding NO-OPs. For image files, we considered changes such as cropping the image, adding small dots and rotating the image. We implemented programs which would automatically modify content in these ways and/or collected data sets where adversaries had used such techniques.

At the high level, we optimised the various parameters of TLSH to be resistant to attack. We will now dig deeper to explain this.

Deep Dive into Robustness

Quick review of the design of TLSH

There are 2 key components for designing a fuzzy hash:
  1. The algorithm to calculate the hash
  2. The form and parameters scoring function that scores the distance between 2 hashes.

Algorithm to Calculate TLSH

The algorithm takes the typical form of a locality sensitive hash. It has 3 notable elements: The choice of a 4 valued vector and 128 bucket counts was to optimise a ROC curve.

Figure 5. ROC Curve
Note: optimising the parameters using the area under a ROC curve means that the method will work with multiple thresholds enabling the fast search described above.

The Choice of Kskip-ngram

We chose to use kskip-ngrams in TLSH because it resulted in an overall design which was as accurate an ngram approaches on baseline data, but was far more resistant to attack when we applied the automated attack methods (as described in Designing the Elements of a Fuzzy Hashing Scheme). we also analysed the computational cost of using kskip-ngrams which grows very quickly as k and n grow. We determined that n=5 and k=2 resulted in an overall design which is both computationally efficient and highly resistant to attack. The resultant features consist of triplets of bytes out of a window of size 5 (features with holes in them) results in an overall design where the impact of minor changes to bytes is reflected in only minor changes in score.

The Scoring Function

The Form of the Scoring Function

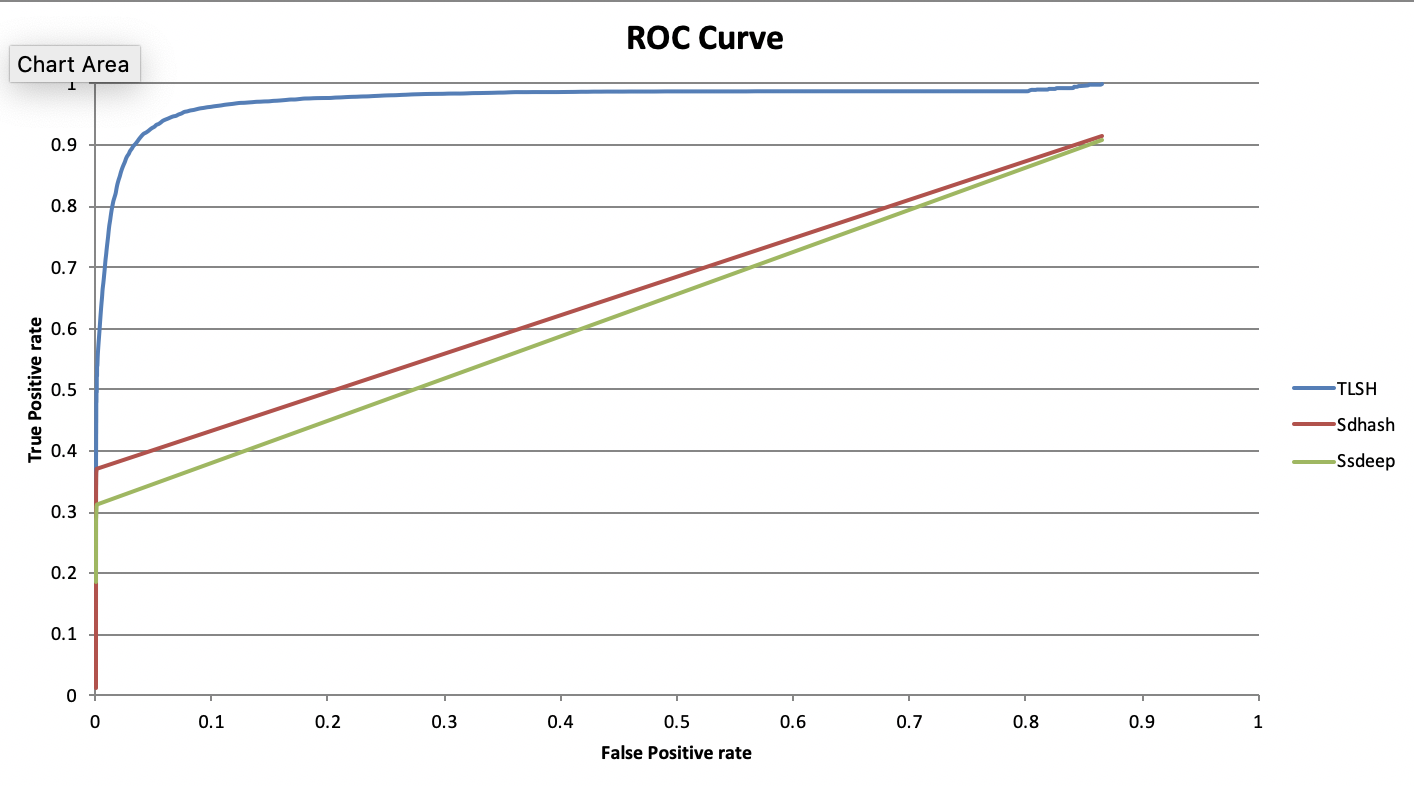
We choose a scoring function which takes the form of a distance metric and not similarity measure so that we could achieve the fast search and scalable clustering as described above.

The Parameters of the Scoring Function

The scoring function has quite a few parameters which people have questioned why they take the value they do (such as the length scoring parameter of 12 and the various distance parmeters).
We choose the parameters of the scoring function (such as 12 for the score per length difference) based on optimising the ROC curve shown above in Figure 5 above. (further details in this paper).

Conclusion

TLSH was designed based on the criteria at the top of this article.

Appendix Summary of Papers

Copyright © 2013-2021 TrendMicro
Last updated on 26/11/2021.